With the latest update of my AHP online software it is now possible to save judgments (pairwise comparisons) without completing the whole hierarchy evaluation. There are two scenarios, where this could be useful:
- You have a complex hierarchy with many nodes to be evaluated. Now participants can start a partial evaluation, save the judgments and complete the remaining nodes at a later time.
- As a participant you are only expert for a subset of nodes in the decision hierarchy. As a chair you can now ask participants to give their inputs for a few nodes of their expertise only.
Pairwise comparison input is started as usually: either using the link provided on the project session page, or using the link AHP Group Session on the AHP-OS main entry page. After providong session code and name, in case the participant hasn’t given any input, a message Ok. Group has x participants. Click “Go” to continue will be displayed. Nodes without judgment show the AHP button with red outline.
Continue reading AHP-OS Hierarchy Evaluation with Partial Inputs from Participants
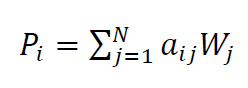
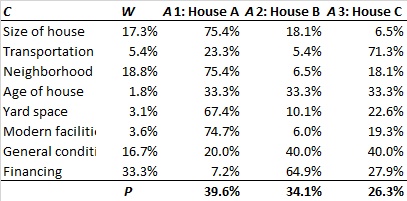

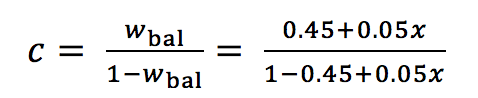
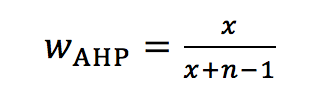
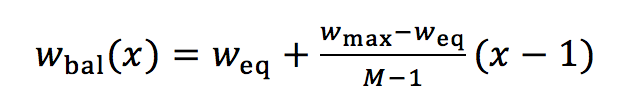 (3)
(3)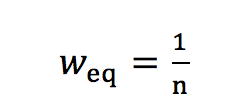 (3a)
(3a)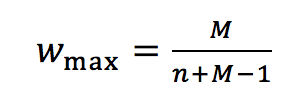 (3b)
(3b)