Since April 2022 a new feature of AHP-OS, Group Consensus Cluster Analysis is available. It can be reached from the AHP-OS main page.
The idea of the program is to cluster a group of decision makers into smaller subgroups with higher consensus. For each pair of decision makers the similarity of priorities is calculated, using Shannon alpha and beta entropy. The result is arranged in a similarity matrix and sorted into clusters of higher similarity based on a consensus threshold.
In order to use the program, you first need to load a priority json file, exported from the AHP-OS Group result menu, containing the priorities of all participants:

Once downloaded to your computer, you can import this file via the Group Consensus Menu:

Click on Browse… to select the file; then click Analyze.The result is structured in
- Input data
- Threshold table
- Result for selected node and a
- Similarity Matrix
Input Data
Project session code, selected node (default: pTot), number of categories, number of participants and scale are shown. pTot stands for the global priorities of a hierarchy.
Threshold Table
The program calculates the number of clusters and number of unclustered participants based on a similarity threshold in the range between 70% and 97.5% in steps of 2.5%. For each step the values are displayed in the threshold table.

Automatically the optimal threshold is determined.

In this case as 0.85 with 2 clusters and no unclustered members. If you want to change, for example the number of clusters to 3, you can enter 0.9 as new threshold in the AHP Group Consensus Menu manually.

In the menu you also find a drop-down selection list for all nodes of the project. With Load new data another json file can be loaded.
Result for selected Node
First the AHP group consensus S* or relative homogeneity S for the whole group is shown, followed by the number of clusters. Next, for each cluster (subgroup) S* or S of the subgroup and the number of members in this cluster are displayed. Individual members are shown with a number and their name. The participants number corresponds to the number displayed on the project result page (Project Participants), so it is easy to select or deselect them by their number on the AHP-OS result page based on the result of the cluster analysis.
Similarity Matrix
The similarity matrix is a visualization of the clusters. Each cell (i,j) contains the AHP consensus S* or relative Homogeneity S for the pair of decision makers i and j in percent. Darker green color means higher values as show in the scale above the matrix. Clusters are always rectangles along the diagonal of the matrix, and are framed by borders.
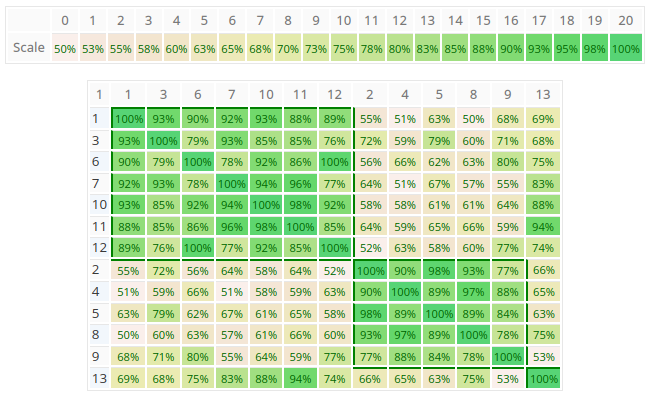
As you can see in the figure above, the program found two clusters with members 1,3,6,7,10,11,12 respectively 2,4,5,8,9, and one unclustered member 13. In this example the group consensus without clustering is 52.4% (low), the consensus for subgroup 1 is 80.5% (high) and subgroup 2 80.7% (high). This means that within the group there are two individual parties in higher agreement. You can easily go back to the project’s group result page to analyze the consolidated priorities for each group by selecting the individual participants.
Once the number of participants exceeds 40, the similarity matrix is shown without values in order to better fit on the output page.

References
Goepel, K.D. (2022). Group Consensus Cluster Analysis using Shannon Alpha- and Beta Entropy. Submitted for publication. Preprint
Goepel, K.D. (2018). Implementation of an Online Software Tool for the Analytic Hierarchy Process (AHP-OS). International Journal of the Analytic Hierarchy Process, Vol. 10 Issue 3 2018, pp 469-487, https://doi.org/10.13033/ijahp.v10i3.590