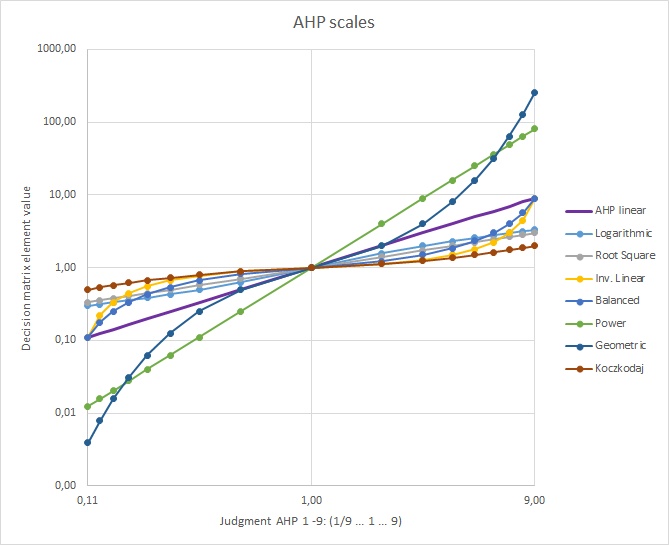
As part of my current work about AHP scales, here an important finding for the balanced scale:
Salo and Hamalainen [1] pointed out that the integers from 1 to 9 yield local weights, which are not equally dispersed. Based on this observation, they proposed a balanced scale, where local weights are evenly dispersed over the weight range [0.1, 0.9]. They state that for a given set of priority vectors the corresponding ratios can be computed from the inverse relationship
r = w / (1 – w) (1a)
The priorities 0.1, 0.15, 0.2, … 0.8, 0.9 lead, for example, to the scale 1, 1.22, 1.5, 1.86, 2.33, 3.00, 4.00, 5.67 and 9.00. This scale can be computed by
wbal = 0.45 + 0.05 x (1b)
with x = 1 … 9 and
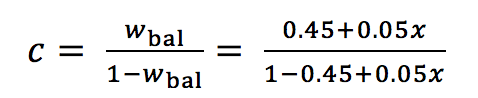 (1c)
(1c)
c ( resp. 1/c) are the entry values in the decision matrix, and x the pairwise comparison judgment on the scale 1 to 9.
In fact, eq. 1a or its inverse are the special case for one selected pairwise comparison of two criteria. If we take into account the complete n x n decision matrix for n criteria, the resulting weights for one criterion, judged as x-times more important than all others, can be calculated as:
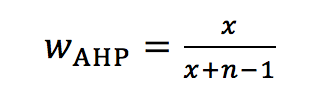 (2)
(2)
Eq. 2 simplifies to eq. 1a for n=2.
With eq. 2 we can formulate the general case for the balanced scale, resulting in evenly dispersed weights for n criteria and a judgment x with x from 1 to M:
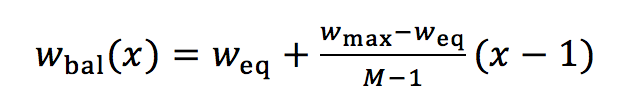 (3)
(3)
with
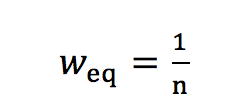 (3a)
(3a)
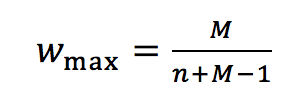 (3b)
(3b)
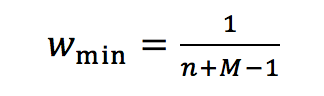 (3c)
(3c)
We get the general balanced scale (balanced-n) as
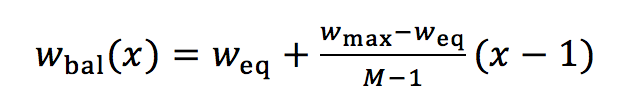 (4)
(4)
Continue reading Why the AHP Balanced Scale is not balanced
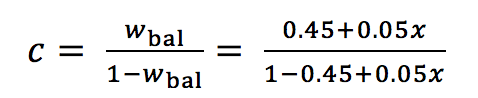
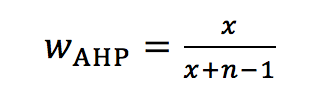
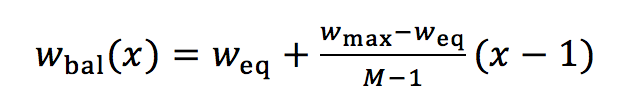 (3)
(3)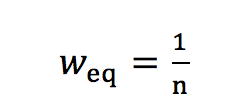 (3a)
(3a)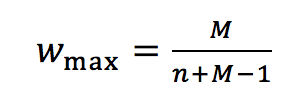 (3b)
(3b)