This was a question in researchgate.net, and the answer of Prof. Saaty – the creator of the method – is of course: “The AHP is the only accurate and rigorous mathematical way known for the measurement on intangibles. It is not going to get old for a long time.“, with a lot of answers from others following.
When it comes to AHP, it seems the scientific world is still divided in opponents and advocates of the method.
I answered with the statistic of my website: BPMSG has more than 4000 users of the online software AHP-OS, 600 of them active users with 1000 projects and more than 3500 decision makers. My AHP excel template reached nearly 21 thousand downloads. It clearly shows that the method is not outdated.
As a reply Nolberto wrote:
“No, I don´t think that AHP is outdated, but the fact that over than 1000 projects have been developed using AHP does not mean that their results are correct (which is impossible to check), or that the method is sound (which is easily challenged)… “
Here my answer:
yes, I agree, the numbers only show that AHP is not outdated (which was the original question). They don’t show, whether the results are correct or incorrect, but they also do not show whether the users did or did not realise the method’s drawbacks and limitations.
For me, as a practitioner, AHP is one of the supporting tools in decision making. The intention of a tool is what it does. A hammer intends to strike, a lever intends to lift. It is what they are made for.
From my users feedback I sometimes get the impression that some of them expect a decision making support tool to make the decision for them, and this is not what it is made for.
In my practical applications AHP helped me and the teams a lot to gain a better insight into a decision problem, to separate important from less important criteria and to achieve a group consensus and agreement how to tackle a problem or proceed with a project. Probably, this could be achieved with other tools too, but as you say, AHP is simple, understandable and easy.
For sure, real world problems are complex. Therefore they have to be broken down and simplified, to be handled with the method, and I agree, over-simplification can be dangerous. On the other hand, what other approach than the break down of complex problems into digestable pieces is possible?
Finally, it’s not the tool producing the decision, but the humans behind it. They will be accountable for the decision, and it’s their responsibility to find the appropriate model of a decision problem and the right balance between rational and non-rational arguments and potential consequences of their decision.
Let me know your opinion!
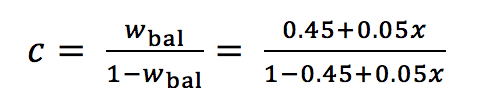
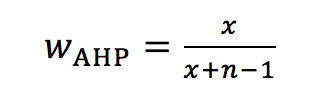
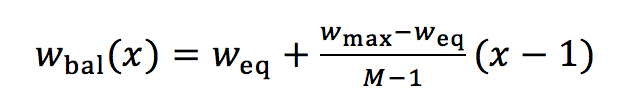 (3)
(3)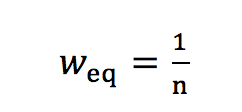 (3a)
(3a)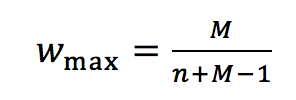 (3b)
(3b)