Concepts, Methods and Tools to manage Business Performance
Dear Friends, dear Visitors,
We released a major update of my free AHP online software. It is now running under PHP 7 and should be noticeable faster than before. Beside some under-the-hood improvement a few new features were added. For more details read my post here.
As a new tool on my website I added a collection of my literature about multi-criteria decision making and AHP. It is available for everyone under the menu point Tools -> Literature. I am using the open source software package Wikindx5. You can browse or search for articles, authors, journals etc. Over time I will fill it up with more article and other research contributions. You can also register as a user and add your own literature to share with others.
Wikindx allows to include citations into a blog. As an example, the following reference is taken from Wikindx:
Many thanks to all donors, supporting this website. Unfortunately, over the last months I didn’t receive many donations. The annual invoice from my hosting provider is expected to come soon, therefore, please continue to support my effort with a small donation, especially when you use my free template or online software.
For now, please enjoy your visit on the site and feel free to leave a comment – it is always appreciated. And keep in mind: Better to be approximately right than precisely wrong.

Klaus D. Goepel, Singapore, July 2019
BPMSG stands for Business Performance Management Singapore. As of now, it is a non-commercial website, and information is shared for educational purposes. Please see licensing conditions and terms of use.




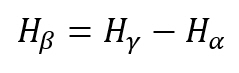
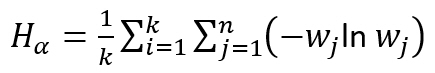
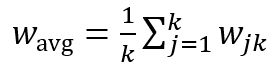
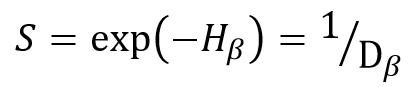
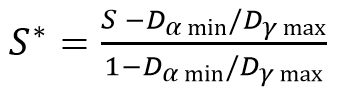
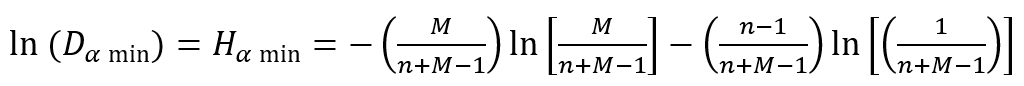
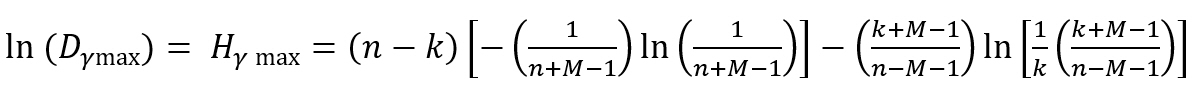
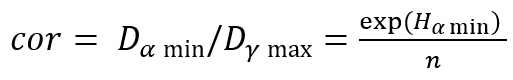
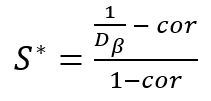 Equation (1.10) is used in the latest updated of the
Equation (1.10) is used in the latest updated of the