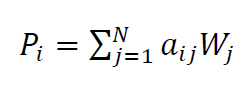As I know from my own experience, manuals are seldomly read. On the other hand, a short guideline to complex software can be helpful, to use it effectively. I summarised the main menus of AHP-OS in a four page quick reference guide. The full manual is still available from the AHP-OS entry page (needs update …), and all details regarding methods and calculations are shown in my working paper about the AHP-OS software implemetation.
The latest update of AHP-OS comprises of some minor changes to make the program flow easier to understand for participants w/o background in AHP.
For anyone, who is interested in the implementation of my free AHP-OS online software, and needs a reference:
Implementation of an online software for the Analytical Hierarchy Process
I hope to finalize the paper soon so that I can submit it for publication.
Sensitivity analysis is a fundamental concept in the effective use and implementation of quantitative decision models, whose purpose is to assess the stability of an optimal solution under changes in the parameters. (Dantzig)
In AHP the preference Pi of alternative Ai is calculated using the following formula (weighted sum model):
(1)
with Wj the weight of criterion Cj, and aij the performance measure of alternative Ai with respect to criterion Cj. Performance values are normalized.
(2)
Example
Sensitivity analysis will answer two questions:
changing the ranking between two alternatives?
The original AHP uses ratio scales. To derive priorities, verbal statements (comparisons) are converted into integers from 1 to 9. This “fundamental AHP scale” has been discussed, as there is no thoretical reason to be restricted to these numbers and verbal gradations. In the past several other numerical scales have been proposed [1],[3]. AHP-OS now supports ten different scales:
Fig. 1 Mapping of the 1 to 9 input values to the elements of the decision matrix.
Most data generated with AHP-OS can be downloaded as csv files for import into a spreadsheet program and further analysis:
For each download you can select “.” or “,” as decimal separator. The downloaded csv (text) file is coded in UTF-8 and supports multi-language characters like Chinese, Korean, Japanese and of course a variety of Western languages.
Open Excel, click on “File” -> “New” to have a blank worksheet. Click on “Data“. On the left top you will find the “Get External Data” box.
Over the year I receive many questions about AHP, my AHP excel template and my AHP online Software. Here a selection of frequently asked questions:
Q: I have 15 criteria and 20 alternatives, can you extend your template/software?
A: The excel template can handle up to 10 criteria, my online software is limited to 12 criteria (in one hierarchy level) and 10 alternatives. In principle it could be extended, but the limitation is inherit to the AHP method. Please read my explanations here.
Q: I have more than 10 alternatives, can I use AHP for priority evaluation of criteria and a different method for the evaluation of alternatives?
A: Yes, you can combine AHP for criteria evaluation with another method for alternative evaluation. Alternative evaluation could be done for example using a simple table with a yes/no or applicable/not applicable scale, or any other scale, e.g. Likert scale, how good the individual alternative matches the specific criterion.
Q: I have 150 participants, can I use your excel template/software?
A: My AHP excel template is limited to 20 inputs, my AHP online software can handle a (practically) unlimited number of participants. Use the AHP online software.
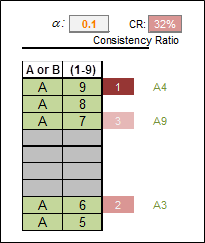
Q: How can I resolve the inconsistency (CR>0.1), when participants are done with their pairwise comparisons.
A: Once the pairwise comparison is done and submitted, data can not be changed and consistency ratio is what it is. Ask your decision makers to adjust their judgments in direction of the most consistent input during the pair-wise comparisons for the highlighted three most inconsistent comparisons. Please see also my posting here.
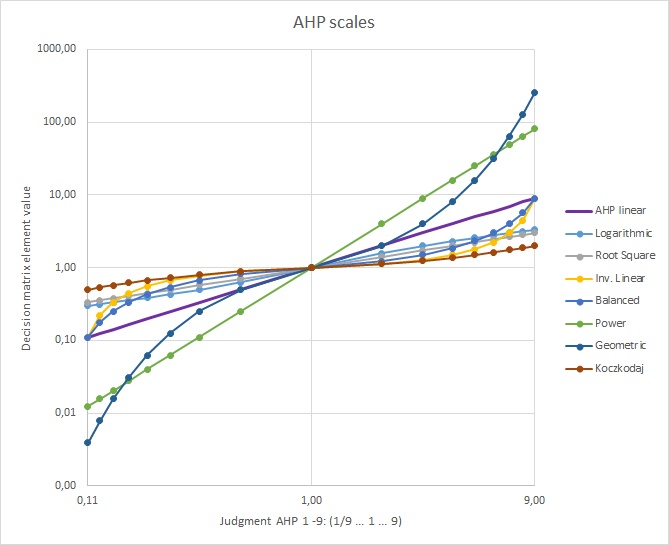
Q: Can I use the Likert scale instead of the AHP scale?
A: No, AHP is based on the rational scale 1/9 … 1 … 9. It cannot be replaced by the Likert scale.
Q: Do you support Fuzzy AHP?
A: No, I have made no provisions to support Fuzzy AHP, neither in Excel, nor in my online software.
Q: How is the computation done, where do I find the description and formulas?
A: Please download the manual for the excel template, or the description about the Software Implementation of AHP-OS.
Q: How can I cite your work, can you give me a reference?
A: Please cite my paper: Implementing the analytic hierarchy process as a standard method for multi-criteria decision making in corporate enterprises–a new AHP excel template with multiple inputs (Excel template) or my paper Software Implementation of AHP-OS.
Q: Can I extend the number of participants to more than 20?
A: Though it is possible in principle, the better way is to use my AHP online software with (practically) unlimited number of participants. I will not do a further extension of the template.
Q: Do you have a version of the Excel template w/o multiple inputs?
A: Yes, a simplified version is available on request from the author.
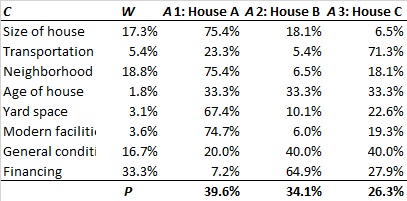
Q: How can I do alternative evaluation using your Excel template.
A: It is not possible. The template can only handle one category of a hierarchy and calculate the priority of one set of criteria.
Q: If I have a group of decision makers, do they need to register for the online software?
A: No, they don’t need to register. As the owner of a project you get a link for group decision inputs. Simply send them the link, and they can start the pairwise comparisons.
Q: Can I erase/delete inputs from individual participants from the group results?
A: Yes, you can select and delete individual participants from a project .
Q: The alternative evaluation is not working?
A: Criteria evaluation (priorities) and alternative evaluation have to be handled as two different projects. Only when you have a decision hierarchy with completed comparisons and evaluated priorities, you can define the alternatives from the group result page clicking on Use consol. priorities. Define number and name of alternatives from there and save as new project. Hierarchy evaluation and alternative evaluation projects appear as type “H” for the first and type “A” for the latter in your project list.
Q: Can I get the source code of your online software?
A: Sorry, it is not an open source project.
Note: All answers assume that you are a registered user and logged in.
Q: How do I save a new AHP hierarchy definition?
A: In the Session Administration Menu click on New.
The hierarchy window is displayed. Define a new hierarchy in the text input field and click on Submit new hierarchy, then Save in the Hierarchy Input Menu.
The group session window will open. Optionally provide a project short description and click Go, and the defined hierarchy is stored and shown as type “H” (Hierarchy) in the project table of the Session Administration Menu.
Q: How can I define and store a project for the evaluation of alternatives?
A: Start with a hierarchy definition, save and resume from the project table by clicking on the session code link. Complete all pairwise comparisons (Click on AHP in the hierarchy) to define the weights of criteria. (Before alternatives can be evaluated, criteria weights need to be defined.) Submit for group evaluation and view the result. In the group result page click on Use consol. priorities.
Then click on Evaluate Alternatives in the decision hierarchy display. Provide number and names of your alternatives and save a new project. It will be saved as type “A” (Alternative Evaluation). From there you can resume and start the alternative evaluation.
Q: How can I use a defined and stored hierarchy definition as template for a new project or new group session?
A: Click on the session code link of the project, you want to use, in the Stored AHP project session table.
a) If the project has no participants, the project will be opened in the group session input mode. Click on Leave, then Close in the Active Session Menu.
b) If the project has participants, the project will be opened in the AHP Group result window. Click on the Resume link at the bottom of the page, then Leave and Close in the Active Session Menu as in a).
You can now re-use the hierarchy definition and save as a new project.
With the latest version of my free AHP software you can manage complete AHP projects, including the handling of group sessions. In order to use the full functionality, you need to register (it’s free). You can find the manual there.
In this latest update of my AHP excel template, input sheets were modified to show the proposed ideal judgments for the three most inconsistent inputs, resulting in a lower consistency ratio CR.
Example
On the left side judgment A9, A7 and A6 are highlighted as inconsistent, CR is 32%. The consistent judgment is shown as A4, A9 and A3. After correction with the proposed intensities (right side) the consistency ratio decreases to 7% below the required threshold of 10%.
You might download the latest version from my AHP template download page.
