AHP stands for analytic hierarchy process, and belongs to the multi-criteria decision making methods (MCDM). In AHP, values like price, weight, or area, or even subjective opinions such as feelings, preferences, or satisfaction, can be translated into measurable numeric relations. The core of AHP is the comparison of pairs instead of sorting (ranking), voting (e.g. assigning points) or the free assignment of priorities.
Read my simple write-up about AHP for people, who have not heared about the method. You might download it as pdf document.
Principia Mathematica Decernendi
or “Mathematical Principles of Decision Making” is the title of a book by Prof. Thomas L. Saaty, in which he describes his method for the mathematical treatment of decision problems, which he developed in the 70s. Called AHP, it is now used around the world in many different fields. AHP stands for analytic hierarchy process, and belongs to the multi-criteria decision making methods (MCDM) group.
In AHP, values like price, weight, or area, or even subjective opinions such as feelings, preferences, or satisfaction, can be translated into measurable numeric relations.
Mathematically, the method is based on the solution of an “eigenvalue problem” – but this is mentioned here only tangentially and is not meant to dissuade anyone.
Analytic hierarchy process
The basic steps in the solution of a decision problem using AHP are quite simple:
- Define the goal of the decision – what do I want to decide, for what purpose, and what are my alternatives?
- Structure the decision problem in a hierarchy – what are the categories and criteria that figure into my decision?
- Pair comparison of criteria in each category – e.g. blue or green? Which do I prefer, and by how much do I prefer one or the other color?
- Calculate the priorities and a consistency index – were my comparisons logical and consistent?
- Evaluate alternatives according to the priorities identified – what alternative optimum solution is there to the decision problem?
Sometimes alternatives are already implicitly defined by the problem and it is sufficient merely to define the priorities.
The core of AHP is the comparison of pairs instead of sorting (ranking), voting (e.g. assigning points) or the free assignment of priorities. Validation of the method in practical testing shows surprisingly good agreement with actual measured values.
One of the most interesting fields and a very current application of AHP is the identification of suspects by witnesses in criminal cases, where the candidates for identification are not shown all together or sequentially, but in pairs. AHP is then used to evaluate the results. Initial studies show that this increases the reliability of identification from 55 % to 83 % and reduces the false identification rate from 20 % to 17 %, and that the consistency index is a good measure of the reliability of statements by witnesses.
Example
To demonstrate how the method works, let us take a simple example. I want to buy an MP3 player. I have the choice of colors (pink, blue, green, black, red), storage (8, 16, 32, 64 Gbyte), and availability (immediate, 1 week, 1 month). The available models are:
- Model A – pink, 32 Gbyte, immediate availability, USD 120
- Model B – blue , 16 Gbyte, immediate availability, USD 120
- Model C – black , 32 Gbyte, 1 week wait, USD 150
- Model D – red, 64 Gbyte, 1 month wait, USD 150
We can structure the problem hierarchically as shown in Fig. 1. In the solution process itself each element is compared by pairs in each category and sub-category, and the criteria are weighted.
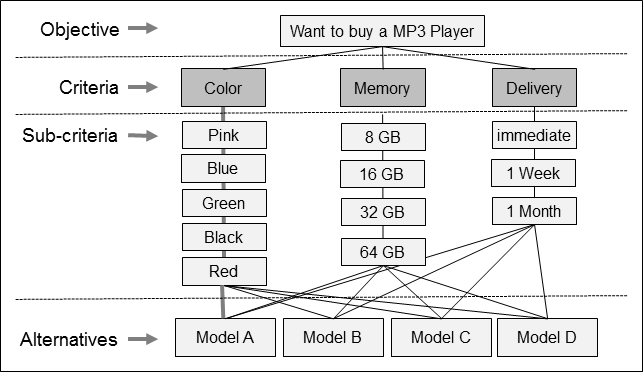
Fig. 1 AHP hierarchy for solving a decision problem
Complex decision problems and networks
For complex decision problems a two-layer model can be introduced, in which hierarchies are examined separately by the criteria Benefits (B), Opportunities (O), Costs (C) and Risks (R). This is known as the BOCR model. The problem is then evaluated using the simple formula (B*O)/(C*R) (multiplicative) or (B+O)-(C-R) (additive).
The analytical network process (ANP) is a further development of AHP. In it, the decision problem is modeled not as a hierarchy, but as a network. However, its practical application and mathematical treatment are much more involved.
Applications
AHP has been used successfully in many institutions and companies. Although the method is so universal, it is still simple enough to execute in Excel. One of AHP’s great advantages is the ability to use it for group decisions, in which all participants evaluate pairs and the group result is determined as the mathematically optimum consensus. In practice the solutions arrived at by the method are well accepted, since the results are objective and free of political influence.
Examples of projects in a business context are the weighting of key performance indicators (KPI) or the identification of key strategies for sustained growth.
Klaus D. Goepel – Singapore Aug 2013.
Calculate priorities using my AHP online calculator or handle a complete AHP project using my AHP online software AHP-OS.
The 12th International Symposium on the Analytic Hierarchy Process – Multi-criteria Decision Making – took place under the theme “Better world through better decision making” from June 23rd to 26th in Kuala Lumpur, Malaysia.
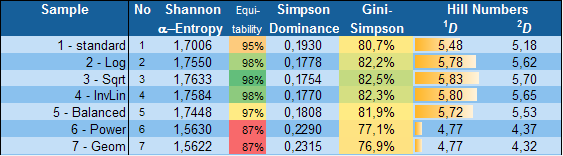
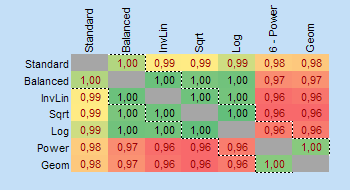The diversity calculator is an excel template that allows you to calculate alpha-, beta- and gamma diversity for a set samples (input data), and to analyze similarities between the samples based on partitioning diversity in alpha and beta diversity.
