Sensitivity analysis is a fundamental concept in the effective use and implementation of quantitative decision models, whose purpose is to assess the stability of an optimal solution under changes in the parameters. (Dantzig)
Weighted sum model (Alternative Evaluation)
In AHP the preference Pi of alternative Ai is calculated using the following formula (weighted sum model):
(1)
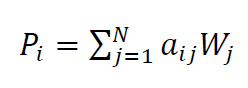with Wj the weight of criterion Cj, and aij the performance measure of alternative Ai with respect to criterion Cj. Performance values are normalized.
(2)
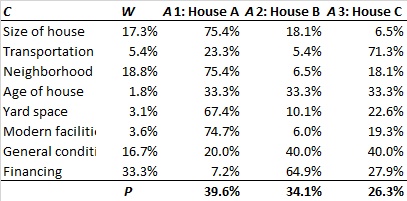
Example
Sensitivity analysis will answer two questions:
- Which is the most critical criterion, and
- Which is the most critical performance measure,
changing the ranking between two alternatives?
The most critical criterion
The most critical criterion is defined as the criterion Ck, with the smallest change of the current weight Wk by the amount of δkij changing the ranking between the alternatives Ai and Aj.
The Absolute-Top (or AT) critical criterion is the most critical criterion with the smallest change δkij changing the ranking of the best (top) alternative.
The Absolute-Any (or AA) critical criterion is the most critical criterion with the smallest change δkij changing any ranking of alternatives.
For each pair of alternatives Ai, Aj, with i = 1 to n and i < j we calculate
(3)
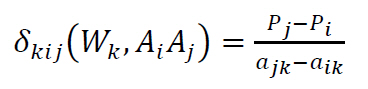with 
.
Example
Table 2
- The absolute-top critical criterion is Neighbourhood: a change from 18.8% by -8% will change the ranking between the top alternative A1 (House A) and alternative A2 (House B).
- The absolute-any critical criterion is the same as above, as -8% is the smallest value in the table.
As the weight uncertainty for the criterion Neighbourhood is +1.4% and -1.3%, the solution is stable.
The most critical measure of performance
The most critical measure of performance is defined as the minimum change of the current value of aij such that the current ranking between alternative Ai and Aj will change.
For all alternatives Ai and Aj with i ≠ j and and each criterion we calculate
(4)
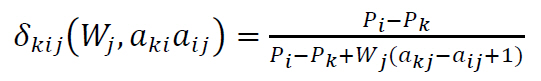
with 
.
Example
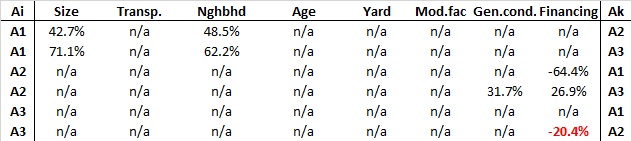Table 3
- The absolute-any critical performance measure is found for alternative A3 (House C) under the criterion Financing. A change from 27.9% by 20.4% will change its ranking with alternative A2 (House B), i.e. only a (drastic) change from 27.9% to 48.3% of the evaluation of House C with respect to Financing would change the ranking of House C and House B.
Implementation in AHP-OS
For alternative evaluation the method described above is implemented in AHP-OS. On the group result page in the Group Result Menu tick the checkbox var and then click Refresh.
Under the headline Sensitivity Analysis TA and AA critical criterion as well as AA critical performance measure will be displayed. You can download the complete tables as csv files with a click on Download.
References
Triantaphyllou, E., Sánchez, A., A sensitivity analysis approach for some deterministic multi-criteria decision making methods, Decision Sciences, Vol. 28, No. 1, pp. 151-194, (1997).