As I was asked by many visitors, how to evaluate priorities and alternatives for a whole project in AHP, I have realized an online solution, where you can define a hierarchy, get the priorities for all categories and evaluate alternatives. The project is realized in PHP.
| AHP Online System – BPMSG |
| AHP-OS software Implementation (paper 2018) |
| Short description (pdf) for download. |
Please rate the software at the end of this post!
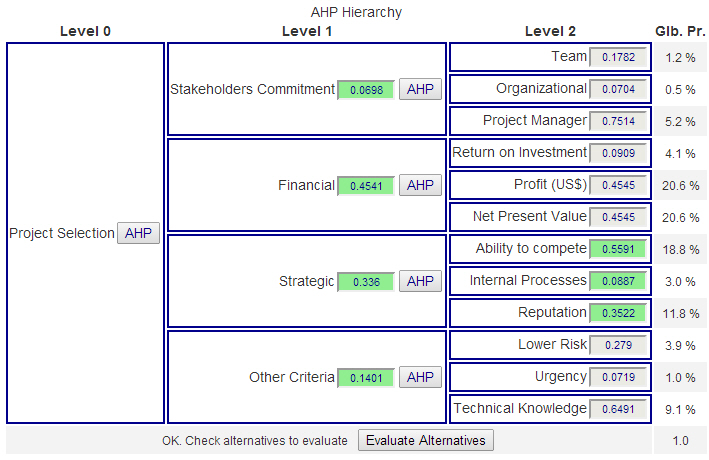
The AHP online calculator is part of BPMSG’s free web-based AHP online system AHP-OS. If you need to handle a complete decision hierarchy, group inputs and alternative evaluation, use AHP-OS.
Calculate priorities from pairwise comparisons using the analytic hierarchy process (AHP) with eigen vector method. Input the number of criteria between 2 and 20 1) and a name for each criterion. Next, do a pairwise comparison: Which of the criterion in each pair is more important, and how many times more, on a one to nine scale. With Check consistency you will then get the resulting priorities, their ranking, and a consistency ratio CR2) (ideally < 10%). Calculation is done using the fundamental 1 to 9 AHP ratio scale.
The three judgments with highest inconsistency will be highlighted, with the last column showing the recommended judgment for lowest consistency ratio. Slightly modify your comparisons, if you want to improve consistency, and recalculate the result, or download the result as a csv file.
Example of inconsistent pair-wise comparisons. The most inconsistent judgment no 2 is marked in red (Color or Delivery); the consistent judgment would be 3 (B) and is highlighted in light green. Decision makers can decide to adjust some of their original judgments to improve consistency.
| Here the link: AHP priority calculator |
Kindly rate the software from 1 star (poor) to 5 stars (excellent) at the bottom of this post.
Please make reference to the author and website, when you use the online calculator for your work. For terms of use please see our user agreement and privacy policy.
Fields are separated by tabs:
1) Though the maximum number of criteria is 15, you should always try to structure your decision problem in a way that the number of criteria is in the range 5 to 9.
2) Alonso, Lamata, (2006). Consistency in the analytic hierarchy process: a new approach. International Journal of Uncertainty, Fuzziness and Knowledge based systems, Vol 14, No 4, 445-459.
