Sensitivity analysis is a fundamental concept in the effective use and implementation of quantitative decision models, whose purpose is to assess the stability of an optimal solution under changes in the parameters. (Dantzig)
Weighted sum model (Alternative Evaluation)
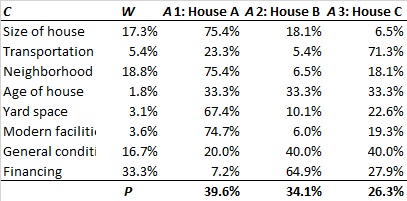
In AHP the preference Pi of alternative Ai is calculated using the following formula (weighted sum model):
(1)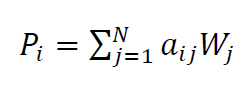 with Wj the weight of criterion Cj, and aij the performance measure of alternative Ai with respect to criterion Cj. Performance values are normalized.
with Wj the weight of criterion Cj, and aij the performance measure of alternative Ai with respect to criterion Cj. Performance values are normalized.
(2)![]()
Example
Sensitivity analysis will answer two questions:
- Which is the most critical criterion, and
- Which is the most critical performance measure,
changing the ranking between two alternatives?